A Complete Overview of D.C. Circuits: Key Concepts and Applications

Introduction

In the previous session we studied about the A Closer Look at Electric Circuits: Exploring the Various Types and Their Applications.Now in this session we study in detail about types of D.C. Circuits and application of it.An electric circuit can be viewed as the core of all advanced technology, delivering the power for our toasters, cars, and even space-faring spacecraft. The basic configuration would include series circuits and parallel circuits that have different properties but are remarkably applicable as based on the significance of the employment.

D.C. Circuit

A direct current circuit, or DC circuit for short, is an electrical circuit in which the electric charge (current) flows only in one direction and remains constant. The voltage across the circuit's terminals in a DC circuit never changes. DC circuits maintain a constant flow of current in a single direction, in contrast to AC (Alternating Current) circuits where the current changes direction on a regular basis.Accordingly, d.c. circuits can be classified as:

Series circuits
Parallel circuits
Series-parallel circuits

D.C. Series Circuit

The d.c. circuit in which resistances are connected end to end so that there is only one path for current to flow is called a d.c. series circuit.

Consider three resistances R1, R2 and R3 ohms connected in series across a battery of V volts as shown in Fig. 1. Obviously, there is only one path for current I i.e. current issame throughout the circuit. By Ohm’s law, voltage across the various resistances is

`V_1=IR_1`;`V_2=IR_2`;`V_3=IR_3`

Now `V=V_1+V_2+V_3`

`=IR_1+IR_2+IR_3`

`=Ileft(R_1+R_2+R_3right)`

or `frac VI=R_1+R_2+R_3`

Figure 1

Figure 2

But V/I is the total resistance `R_s` between points A and B. Note that `R_s` is called the total or
equivalent resistance of the three resistances.

∴`R_s`=`R_1`+`R_2`+`R_3`

Hence when a number of resistances are connected in series, the total resistance is equal to the sum of the individual resistances.

The total conductance `G_s` of the circuit is given by ;

`G_s=frac1{R_s}=frac1{R_1+R_2+R_3}`

Also `frac1{G_S}=frac1{G_1}+frac1{G_2}+frac1{G_3}`

The main characteristics of a series circuit are:

The current in each resistor is the same.
The total resistance in the circuit is equal to the sum of individual resistances.
The total power dissipated in the circuit is equal to the sum of powers dissipated in
individual resistances. Thus referring to Fig. 1,

`R_s=R_1+R_2+R_3`

or `I^2R_s=I^2R_1+I^2R_2+I^2R_3`

or `P_s=P_1+P_2+P_3`

Thus total power dissipated in a series circuit is equal to the sum of powers dissipated in individual resistances. As we shall see, this is also true for parallel and series-parallel d.c. circuits.

Note. A series resistor circuit [See Fig. 1] can be considered to be a voltage divider circuit because the potential difference across any one resistor is a fraction of the total voltage applied acrossthe series combination;the fraction being determined by the values of the resistances.

D.C. Parallel Circuit

When one end of each resistance is joined to a common point and the other end of each resistance is joined to another common point so that there are as many paths for current flow as the number of resistances, it is called a parallel circuit.

Consider three resistances `R_1`, `R_2` and `R_3` ohms connected in parallel across a battery of V volts as shown in Fig. 3. The total current I divides into three parts: `I_1` flowing through `R_1`, `I_2`flowing through `R_2` and `I_3` flowing through `R_3`. Obviously, the voltage across each resistance is the same (i.e. V volts in this case ) and there are as many current paths as the number of resistances. By Ohm’s law, current through each resistance is

`I_1=frac V{R_1}`;`I_2=frac V{R_2}`;`I_3=frac V{R_3}`

Now `I=I_1+I_2+I_3`

`=frac V{R_1}+frac V{R_2}+frac V{R_3}`

`=Vleft(frac1{R_1}+frac1{R_2}+frac1{R_3}right)`

Figure 3

Figure 4

`frac IV=frac1{R_1}+frac1{R_2}+frac1{R_3}`

But `frac VI` is equivalent resistance `R_p` of the parallel resistances [See Fig. 4] so that `frac IV` = `frac1{R_p}`.

∴`frac1{R_p}=frac1{R_1}+frac1{R_2}+frac1{R_3}`

Hence when a number of resistances are connected in parallel, the reciprocal of total resistance is equal to the sum of the reciprocals of the individual resistances.

Also `G_p=G_1+G_2+G_3`

Hence total conductance `G_p` of resistors in parallel is equal to the sum of their individual conductances.

We can also express currents `I_1`, `I_2` and `I_3` in terms of conductances.

`I_1=frac V{R_1}=VG_1=frac I{G_p}times G_1=Itimesfrac{G_1}{G_p}=Itimesfrac{G_1}{G_1+G_2+G_3}`

Also `I_2``=Itimesfrac{G_1}{G_1+G_2+G_3}` and `I_3``=Itimesfrac{G_1}{G_1+G_2+G_3}`

Main Features of Parallel Circuits

The voltage across each resistor is the same.
The current through any resistor is inversely proportional to its resistance.
The total current in the circuit is equal to the sum of currents in its parallel branches.
The reciprocal of the total resistance is equal to the sum of the reciprocals of the individual
resistances.
As the number of parallel branches is increased, the total resistance of the circuit is
decreased.
The total resistance of the circuit is always less than the smallest of the resistances.
If n resistors, each of resistance R, are connected in parallel, then total resistance `R_p` = `frac Rn`.
The conductances are additive.
The total power dissipated in the circuit is equal to the sum of powers dissipated in the
individual resistances. Thus referring to Fig. 3,

`frac1{R_p}=frac1{R_1}+frac1{R_2}+frac1{R_3}`

or `frac{V^2}{R_p}=frac{V^2}{R_1}+frac{V^2}{R_2}+frac{V^2}{R_3}`

or `P_p=P_1+P_2+P_3`

Like a series circuit, the total power dissipated in a parallel circuit is equal to the sum of powers dissipated in the individual resistances.

Note. A parallel resistor circuit [See Fig. 3] can be considered to be a current divider circuit because the current through any one resistor is a fraction of the total circuit current; the fraction depending on the values of the resistors.

Two Resistances in Parallel

A frequent special case of parallel resistors is a circuit that contains two resistances in parallel.Fig. 5 shows two resistances `R_1` and `R_2` connected in parallel across a battery of V volts. The total current I divides into two parts ; `I_1` flowing through `R_1` and `I_2` flowing through `R_2`.

1.Total resistance `R_p`.`frac1{R_p}=frac1{R_1}+frac1{R_2}=frac{R_1+R_2}{R_1R_2}`

∴`R_p`=`frac{R_1R_2}{R_1+R_2}=frac{Product}{Sum}`

Hence the total value of two resistors connected in parallel is equal to the product divided by the sum of the two resistors.

Figure 5

2.Branch Currents.`R_p`=`frac{R_1R_2}{R_1+R_2}`

`V=IR_p=Ileft(frac{R_1R_2}{R_1+R_2}right)`

Current through `R_1`,`I_1`=`frac V{R_1}=Ileft(frac{R_2}{R_2+R_1}right)` [Putting `V=Ileft(frac{R_2}{R_2+R_1}right)`]

Current through `R_2`,`I_2`=`frac V{R_2}=Ifrac{R_1}{R_1+R_2}`

Hence in a parallel circuit of two resistors, the current in one resistor is the line current (i.e.total current) times the opposite resistor divided by the sum of the two resistors.

We can also express currents in terms of conductances,

`G_p=G_1+G_2`

`I_1=frac V{R_1}=VG_1=frac I{G_p}times G_1=Itimesfrac{G_1}{G_p}=Itimesfrac{G_1}{G_1+G_2}`

`I_2=frac V{R_2}=VG_2=frac I{G_p}times G_2=Itimesfrac{G_2}{G_p}=Itimesfrac{G_2}{G_1+G_2}`

Note. When two resistances are connected in parallel and one resistance is much greater than the other,then the total resistance of the combination is very nearly equal to the smaller of the two resistances.For example, if `R_1` = 10 Ω and `R_2` = 10 kΩ and they are connected in parallel, then total resistance `R_p` of the combination is given by;

`R_p=frac{R_1R_2}{R_1+R_2}=frac{10times10^4}{10+10^4}=frac{10^5}{10010}`= 9.99Ω ⋍ `R_1`

In general, if `R_2` is 10 times (or more) greater than `R_1`, then their combined resistance in parallel is nearly equal to `R_1`.

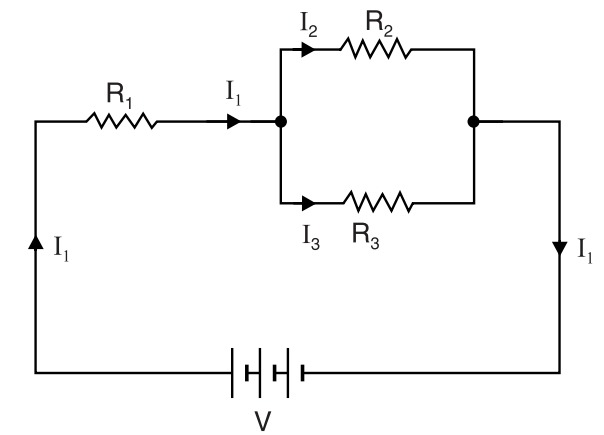
D.C. Series-Parallel Circuit

As the name suggests, this circuit is a combination of series and parallel circuits. A simple example of such a circuit is illustrated in Fig. 6. Note that `R_2` and `R_3` are connected in parallel with each other and that both together are connected in series with `R_1`. One simple rule to solve such circuit is to first reduce the parallel branches to an equivalent series branch and then solve the circuit as a simple series circuit.

Figure 6

Referring to the series-parallel circuit shown in Fig. 6,

`R_p` for parallel combination=`frac{R_2R_3}{R_2+R_3}`

Total circuit resistance=`R_1+frac{R_2R_3}{R_2+R_3}`

Voltage across parallel combination=`I_1timesfrac{R_2R_3}{R_2+R_3}`

The reader can now readily find the values of `I_1`, `I_2`,`I_3`.

Like series and parallel circuits, the total power dissipated in the circuit is equal to the sum of powers dissipated in the individual resistances i.e.,

Total power dissipated, P = `I_1^2R_1`+`I_2^2R_2`+`I_3^2R_3`

Advantages of Parallel Circuits

The most useful property of a parallel circuit is the fact that potential difference has the same
value between the terminals of each branch of parallel circuit. This feature of the parallel circuit
offers the following advantages :

The appliances rated for the same voltage but different powers can be connected in parallel
without disturbing each other’s performance. Thus a 230 V, 230 W TV receiver can be
operated independently in parallel with a 230 V, 40 W lamp.
If a break occurs in any one of the branch circuits, it will have no effect on other branch
circuits.

Due to above advantages, electrical appliances in homes are connected in parallel. We can
switch on or off any light or appliance without affecting other lights or appliances.

Applications of Parallel Circuits

Most household electrical wiring, such as receptacle outlets and lightning system typically uses parallel circuits.
Design of many electrical components such as- different kind of computer hardware is also based on parallel circuit.
In lightning systems, such as in a house or on a Christmas tree, often consists of multiple number of lamps connected parallelly.
In car system, dc power supply works parallelly.
Parallel circuits are one of the main building blocks used in the infrastructure that supplies power to large populations.

Key Difference between Series & Parallel DC Circuit

Now that we've covered the basics of series and parallel DC circuits, let's summarize the key differences between them:Now that we've covered the basics of series and parallel DC circuits, let's summarize the key differences between them.

Current Flow: In the series circuit there is a single path of current flow, while in the parallel circuit one will have various paths of current flow.
Voltage Distribution: In series circuits the voltage divides to the parts of screen while in parallel circuits each part gets the full voltage.
Total Resistance: Resistance in series type circuits is the sum of all the single resistances whereas, resistance of parallel type is calculated somehow alternative ways resulting from multiple paths.
Practical Applications: Series circuits are good for those applications in which the shared primary component current is crucial for all the components. The parallel circuits, however, are best for the cases of the independent component operations.

Conclusion

Becoming aware of the distinction between the D.C. circuits in a series and a parallel streams is essential to creating and fixing electrical systems. The ability to comprehend whether to employ series connection, or parallel one is a threshold in case of simple lighting circulation, or the complex electronic device in order to optimize the operation and guarantee the effective functioning. Gaining a perfect grasp of what is presented on this blog will arm you with the tools needed to deal with electricity circuits challenges, with quality and certainty.